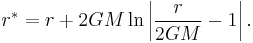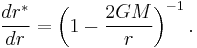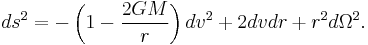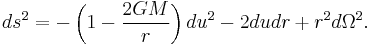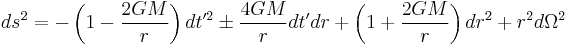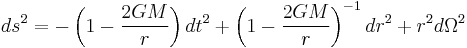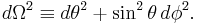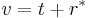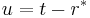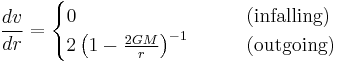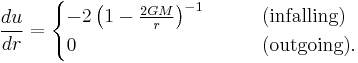Eddington–Finkelstein coordinates

In general relativity Eddington–Finkelstein coordinates, named for Arthur Stanley Eddington and David Finkelstein, are a pair of coordinate systems for a Schwarzschild geometry which are adapted to radial null geodesics (i.e. the worldlines of photons moving directly towards or away from the central mass). One advantage of this coordinate system is that it shows that the apparent singularity at the Schwarzschild radius is only a coordinate singularity and not a true physical singularity.

Contents

Tortoise coordinate

Eddington-Finkelstein coordinates are founded upon the tortoise coordinate.

The tortoise coordinate 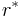r^* is defined:

r^* = r %2B 2GM\ln\left|\frac{r}{2GM} - 1\right|.

so as to satify:

\frac{dr^*}{dr} = \left(1-\frac{2GM}{r}\right)^{-1}.

The tortoise coordinate approaches −∞ as r approaches the Schwarzschild radius r = 2GM.

When some probe (such as a light ray or an observer) approaches a black hole event horizon, its Schwarzschild time coordinate grows infinite. (This is why information would never be received back from any probe that is sent sufficiently close to such an event horizon, despite that the probe itself can nonetheless travel past this horizon. It is also why the metric, expressed in Schwarzschild coordinates, becomes singular at the horizon - thereby failing to be able to fully chart the trajectory of the infalling probe.) The tortoise coordinate is intended to grow infinite at the appropriate rate such as to cancel out this singular behaviour in coordinate systems constructed from it.

Metric

The ingoing Eddington–Finkelstein coordinates are obtained by replacing t with v. The metric in these coordinates can be written

ds^{2} = -\left(1-\frac{2GM}{r} \right) dv^2 %2B 2 dv dr %2B r^2 d\Omega^2.

Likewise, the outgoing Eddington–Finkelstein coordinates are obtained by replacing t with u. The metric is then given by

ds^{2} = -\left(1-\frac{2GM}{r} \right) du^2 - 2 du dr %2B r^2 d\Omega^2.

In both these coordinate systems the metric is explicitly non-singular at the Schwarzschild radius (even though one component vanishes at this radius, the determinant of the metric is still non-vanishing).

Note that dv/dr and du/dr approach 0 and ±2 at large r, not ±1 as one might expect. In Eddington-Finkelstein diagrams, surfaces of constant u or v are usually drawn as cones rather than planes (see for instance Box 31.2 of MTW). Some sources instead take 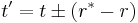t' = t \pm (r^* - r)\,, corresponding to planar surfaces in such diagrams. In terms of this 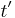t' the metric becomes

ds^2 = - \left( 1-\frac{2GM}{r} \right) dt'^2 \pm \frac{4GM}{r} dt' dr %2B \left( 1 %2B \frac{2GM}{r} \right) dr^2 %2B r^2 d\Omega^2

which is Minkowskian at large r.

Relation to Schwarzschild coordinates

The Schwarzschild coordinates are 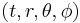(t,r,\theta,\phi), and the Schwarzschild metric is well known:

ds^{2} = -\left(1-\frac{2GM}{r} \right) dt^2 %2B \left(1-\frac{2GM}{r}\right)^{-1}dr^2%2B r^2 d\Omega^2

where

d\Omega^2\equiv d\theta^2%2B\sin^2\theta\,d\phi^2.

Note the conventions being used here are the metric signature of (− + + +) and the natural units where c = 1 (although the gravitational constant G will be kept explicit, and M will denote the characteristic mass of the Schwarzschild geometry).

The ingoing and outgoing null coordinates are defined:

v = t %2B r^*\,
u = t - r^*\,

These are so named because the ingoing radial null geodesics are given by v = constant, while the outgoing ones are given by u = constant.

In ingoing coordinates the equations for the radial null curves are

\frac{dv}{dr} = \begin{cases}0 &\qquad \mathrm{(infalling)} \\ 2\left(1-\frac{2GM}{r}\right)^{-1} &\qquad \mathrm{(outgoing)}\end{cases}

while in outgoing coordinates the equations are

\frac{du}{dr} = \begin{cases}-2\left(1-\frac{2GM}{r}\right)^{-1} &\qquad \mathrm{(infalling)} \\ 0 &\qquad \mathrm{(outgoing).}\end{cases}

See also